Introduction

Psychophysics studies the relationship between physical properties of the world and our psychological perception of them.

A very basic psychophysical experiment, described in the textbook, would involve playing tones of varying volume and asking experiment participants to say whether they hear the tone or not. Based on their responses, we could calculate each subject’s hearing threshold—the volume level at which they can just barely hear the tone.

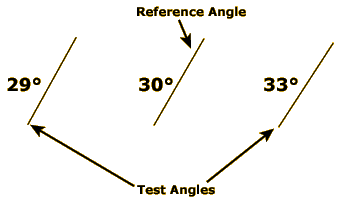
In this activity, we’ll conduct a psychophysical experiment using the 100-pixel-long lines shown at left. The central line in this illustration is rotated 30° clockwise from vertical. We’ll use this as our reference angle. The leftmost line is rotated 29° from vertical—one degree away from the reference angle. The rightmost line is rotated 33° from vertical—three degrees away from the reference.

The psychophysical question we will be asking is how well your visual system can discriminate the angular differences between the reference line and the subtly rotated test lines (either –1° or +3° from the test line).

Go ahead and start the experiment now by clicking the “Start or Restart Experiment” link in the left-side menu.

After you have done a few trials, read about bias in psychophysics experiments and how signal detection theory accounts for it.

Instructions

Click the “Start or Restart Experiment” link on the left side of the screen to get to the experimental part of the activity. Then click the START button to begin a trial. After a brief delay, you’ll see three diagonal lines. The middle line may or may not be exactly the same angle as the two outer lines. Click the appropriate link below the START button to register your guess.

An Example

To better understand the issue of stereoscopic correspondence, consider the small sections of the images at the very tip of the teapots’ spouts, highlighted here by blue and yellow circles. The blue-outlined spout in the left eye should be paired with the blue-outlined spout in the right eye, while the two yellow-outlined spouts should be paired with each other. In other words, the blue-outlined spouts correspond to each other, as do the yellow-outlined spouts.

But how does the visual system know this? Why doesn’t it sometimes match the blue-outlined spout in the left eye with the yellow-outlined spout in the right eye? Determining which points in the left eye to match with which points in the right eye is known in the perception literature as the correspondence problem. While this is a “problem” for the researchers studying it and the teachers trying to explain it, stereoscopic correspondence obviously isn’t all that problematic for the visual system—if it were, we wouldn’t be very good at seeing things in depth!

Your first instinct may be to think that each position on the left retina should just automatically match up to the same position on the right retina. But remember that the whole point of binocular disparity is that most of the objects in your visual field do not fall on corresponding retinal points.

The next most obvious solution is to hypothesize that the visual system first analyzes the shapes of objects in each eye’s image, and then matches shapes across the two images. If we first recognized that there were two teapots in each eye’s image, we could then reason that the left-hand teapot in the left eye probably goes with the left-hand teapot in the right eye. Prior to the 1970s, this was how researchers believed the visual system proceeded. But all this changed when random dot stereograms were introduced to the field.

Start or Restart Experiment

On each trial of our psychophysics experiment, you will see three lines. The outer two lines will always be rotated 30° clockwise from vertical (remember, this is our reference angle). The inner line may be identical to the outer lines, or it may be rotated away from these reference lines by 1° or 3°.

Examine the stimuli as long as you like, then click one of the two links to say whether you think the middle line is the same as or different than the outer lines. If you’re not sure, take a guess.

Click the START button to start a new trial.

You can reset your results if you wish.

Results

The Experiment

Examine the stimuli as long as you like, then click one of the two links to say whether you think the middle line is the same as or different than the outer lines. If you’re not sure, take a guess.

The Experiment

Examine the stimuli as long as you like, then click one of the two links to say whether you think the middle line is the same as or different than the outer lines. If you’re not sure, take a guess.

You must click one of the two links before starting a new trial.

Bias and Signal Detection Theory

As we noted in the introduction, a basic psychophysical experiment might involve playing tones of varying volume and asking experiment subjects to report when they do or do not hear the tone.

If we were to apply this “classical” psychophysical method to the stimuli in this activity, the middle line would always be misaligned relative to the outer lines. We would then vary the degree of misalignment back and forth until we found the angle at which you were just able to detect that the middle line was misaligned.

One problem with this kind of method is that subjects may be (and indeed, usually are) biased to respond in one way or the other. For example, if an observer knows he has poor vision, he may have little confidence in his ability to do the task, so he may always respond that he thinks the lines are perfectly aligned, even when he does sometimes have an inkling that the lines look misaligned. On the other hand, a hot-shot observer may claim to always see the misalignment, even when the lines are so similar that there’s no way her visual system could have detected it.

A good way to address the bias issue is to modify the experimental procedure slightly as we’ve done here, so that on half of the trials the lines really are perfectly aligned. In this modified procedure, the task is no longer to say whether or not you can see the misalignment, but whether or not the lines really are misaligned (this is a subtle, but important, distinction).

If the lines are different enough, an observer should always be able to accurately say whether or not the middle one is misaligned, so she will be accurate 100% of the time. But if the misalignment is near the threshold of vision for this task, the observer will have to guess most of the time, so her accuracy level would be close to 50%. Furthermore, the subject who always claims to see a misalignment would end up with the same overall score (50% correct) as the subject who always claims the lines are identical (think about this for a moment and you should see why).

This modification turns the experiment into a signal detection experiment. The signal is a misaligned center line, and the experimental question is how much orientation difference is needed so that the subject can reliably detect the signal. The outcome of each trial is classified according to the table at left:

If the center line really is misaligned and you correctly say it is misaligned, that is a hit.

If the center line is really identical to the outer lines, but you incorrectly say it is misaligned, that is a false alarm.

If the center line is misaligned but you incorrectly say the three lines are identical, that is a miss.

Finally, if the center line is really identical to the outer lines and you correctly say they are identical, that is a correct rejection.

Signal detection theorists have developed statistical tools for using hit, false alarm, miss, and correct rejection rates to distinguish an observer’s bias from their sensitivity—the true measure of their perceptual ability to do the task at hand. The calculation of these statistics is beyond the scope of this textbook but the basic concept should be fairly easy to understand.

However, if you do enough trials of our experiment you should find that your hit rate for 3°-misaligned central lines is greater than your hit rate for 1°-misaligned central lines, since your visual system is almost certainly more sensitive to larger misalignments than to smaller misalignments. View your results so far and see if this is the case.