Introduction

As Douglas Adams wrote in The Hitchhiker’s Guide to the Galaxy, “It is an important and popular fact that things are not always what they seem.” This activity will demonstrate this fact in various ways.

Instructions

Each part of the activity contains multiple images. Click on the images to toggle between them (image numbers referred to in the explanations wilh appear above the images). The first time you do this activity, you should probably go through the parts in order from top to bottom.

The Necker Cube

“Seeing is believing.” “A picture is worth a thousand words.” These common metaphors attest to the fact that most people consider vision to be the ultimate arbiter of truth. In fact, however, every visual scene is consistent with a number of “truths”. The two-dimensional images that our eyes sense are incapable of providing us with a perfect understanding of the three-dimensional world. In other words, visual perception is inherently ambiguous. Luckily, the human visual system is fantastically good at interpreting visual input in such a way that this ambiguity is (usually) resolved. Nevertheless, the ambiguity is always there, as you will see in this activity.

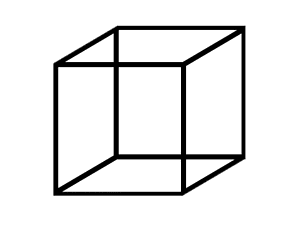
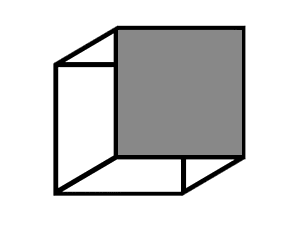
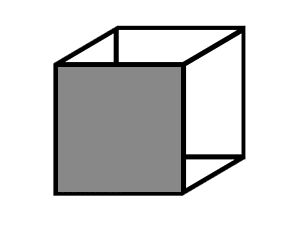
Image 1 at left shows a classic figure, the Necker cube, which was specifically designed to have two different visual interpretations. You will almost certainly interpret the figure as a three-dimensional wire-frame cube, but you may perceive the cube facing up and to the right or down and to the left. Image 2 and Image 3 (click on the cube to toggle between the three images) will bias you toward one interpretation or another. In Image 2, you should find it difficult (if not impossible) to see the cube facing down and to the left, whereas in Image 3 the up and to the right interpretation should be more difficult to see.

Interestingly, while Image 1 allows for two interpretations, it seems impossible to perceive both interpretations simultaneously. If you stare at the figure for a while, you will probably see it “flip” back and forth from facing up-right to down-left, but you cannot see it facing both directions at once. Furthermore, it is difficult to perceive any kind of intermediate interpretation. This demonstrates the visual system’s decisiveness in resolving ambiguity, an extremely adaptive quality. We don’t have the brain power to consider all the possible interpretations of a visual scene simultaneously, so we wisely limit our consideration to one and only one interpretation at a time.

More Ambiguous Figures

This part of the activity includes three more classic ambiguous figures. Image 1 shows the Schröder staircase. Initially, you will probably see this image as a staircase seen from above, with the green wall closer to you, the purple wall farther away, and the pinkish sides of the steps facing upwards. However, it is also possible to see the image flip so that the purple wall appears to be in front, the green wall appears farther away, and the pink sides of the steps are facing down—as if you’re viewing a set of cellar stairs from below. As with the Necker cube, it is impossible to interpret the image in both ways at the same time.

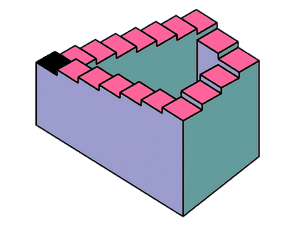
Image 2 shows the “never-ending staircase” design popularized in several etchings by M. C. Escher (click here to see some Escher drawings, including one of Escher’s versions of this figure). At first, nothing seems terribly odd about this figure. However, if you begin at the black step and move clockwise, you will see that the steps go continually down, but eventually return to the black step! Likewise, you can move counterclockwise and step up forever.

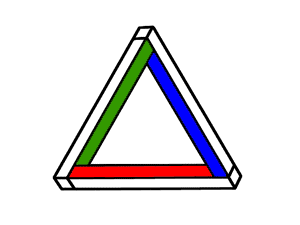
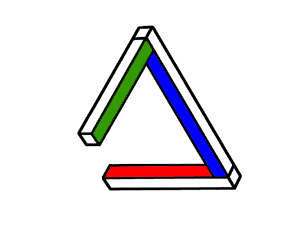
Although it seems impossible, this structure could actually be built, in a way. To understand how, consider Image 3 which shows a simpler, but structurally similar “impossible figure” first conceived in the 1930s. Looking at the top point of the triangle in this image. The green surface occludes the blue surface; therefore, green must be in front of blue. But in the lower part of the triangle, blue appears to be in front of red and red appears to be in front of green. If you think about this situation, it cannot be: if green is in front of blue and blue is in front of red, then green must also be in front of red.

Image 4 shows a similar figure that provides a clue to what’s going on. Here, the green stick appears to be pointing out toward you in three dimensions, with the blue surface angling back and the red surface lying farthest away. You should be able to see that if you extended the green and red surfaces so that they appeared to touch each other, you would get the figure shown in Image 3. Thus the structure in Image 3 is not impossible. Rather, it is a possible object seen from a very strange viewpoint, one in which the green and red sticks appear to intersect each other even though they do not actually meet in three dimensions. Read more about such accidental views in the other parts of this activity.

Accidents of Viewpoint

Here you see an image that looks for all the world like a painting of a flat, two-dimensional pinwheel shape with a yellow background, hanging on a wall across the room from the camera’s position (Image 1). Click on the image to see a movie showing the camera shifting to a side view of the scene, which reveals a very different interpretation: four separate surfaces, suspended in midair at different distances from the viewer and each oriented at a different angle (Image 2).

The initial image is an extreme case of an accidental view of a scene. From this camera position, and only from this camera position, do the green, purple, red, and blue surfaces appear to touch each other and lie in the same plane. When we shift viewpoints even just a little bit (see Image 3), our visual system begins to resolve the situation and perceive the scene “correctly.” Viewpoints that reveal the true structure of a scene are called generic views, whereas viewpoints that obscure the true structure of a scene are called accidental views. However, the line between accidental and generic views is fuzzier than one might think, as shown in the next part of the activity.

Accidental and Ambiguous Views

The images in this part of the activity show an object that you may never have encountered before (it is a push-rider for toddlers). Image 1 shows an accidental view of the object, a photo taken from dead-center in front of the object. From this view, the front of the object appears to be flat, it appears to have only two wheels, and we cannot tell how far back the object extends. In contrast, the photo in Image 2 is taken from a generic viewpoint. Here you seem to get a much better idea of what the structure of the object is really like: the front is actually curved, the object is shown to have both front and back wheels, and a seating area is perceived between the handlebar and the white part at the object’s rear.

Now consider Image 3. We wouldn’t want to call this an accidental view, but it doesn’t seem to be as “good” a view as the one in Image 2. Most strikingly, the object does not appear to be as long in Image 3 as it did in Image 2. On the other hand, Image 3 proves that the object has at least three wheels; in Image 2, only two wheels are actually shown (we infer the existence of four wheels in both images because the object appears to be symmetrical). Moreover, both Image 2 and Image 3 appear to underestimate the true length of the object once the top view of the object (which is technically another accidental view) is seen in Image 4.

These images demonstrate that every view of every object is ambiguous in some way or another. Indeed, architects use accidental views—top, front, and side—to construct their plans for buildings. While each of these views alone does a terrible job of showing the overall structure of a planned building, at least they each reveal precise information about some aspects of the building.

Real World Ambiguity

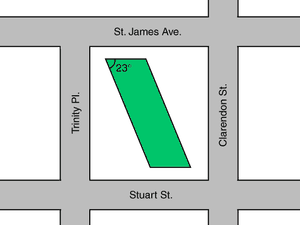
This part of the activity shows one more example of object ambiguity. All the photos here show Boston’s John Hancock Tower, the tallest building in New England. From the viewpoints of Images 1 and 2, the building appears to be more-or-less rectangular. In fact, however, the angles of the building are nowhere near 90 degrees. Image 3 shows a schematic top-view of the building, revealing that the walls intersect at an approximately 23 degree angle on two corners (the other two corners are about 157 degrees). Image 4 shows two photos taken from right beside the building, showing the acute and obtuse angles of two corners. Even when seen from more generic viewpoints than those represented in Images 1 and 2, we have a strong bias to “normalize” our perception of this building, since the vast majority of buildings in Western civilization are constructed with right angles only.