Notes, Chords, and Octaves

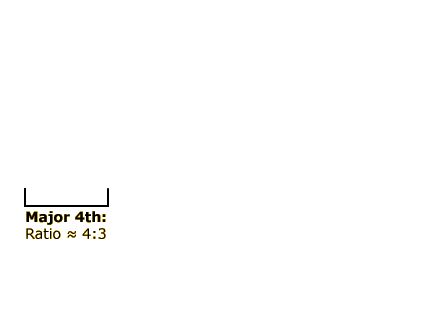
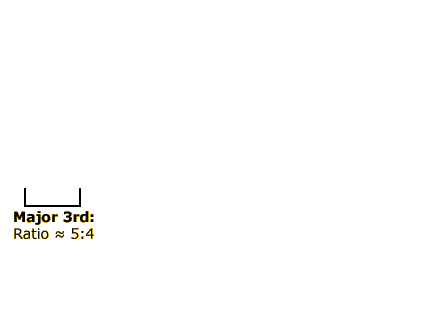





Introduction
In previous chapters, we’ve used the term pitch to refer to the psychological quality associated with the physical property of sound frequency. We’ve learned that as frequency increases, pitch rises.
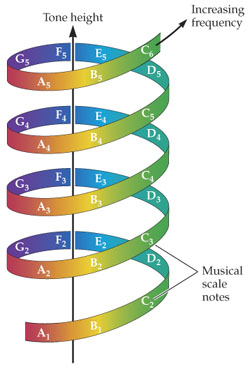
This clear relationship between frequency and pitch gets muddied a bit in this chapter as we consider music perception. Musical pitch (the pitch of a musical note) has two different dimensions, illustrated by the helix at right. As frequency rises, the dimension called tone height rises right along with it. But the second dimension, tone chroma, is cyclical in nature. Western musicians label tone chromas with the letters A–G. As we move from the bottom of the helix up, tone chroma repeats at regular intervals. Thus we see that as we move from C3 to D3 to E3 and on up, we eventually come back to another C (C4).
These repetitions occur at intervals called octaves. If one note is exactly double the frequency of the other note, then the two notes are separated by one octave and have the same tone chroma.
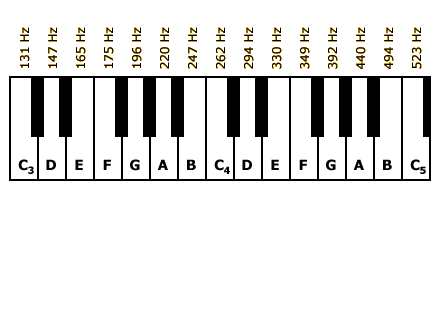
You can experience the psychological similarity of notes with the same and different chromas using the keyboard at left. Start with the lowest note (C3; click on the piano key with this label to play the note), then compare this note with C4 and C5. Now play C3 again, then play F#3 (the black key in between the first F and the first G; the “#” symbol indicates a sharp). Despite the fact that C3 and F#3 are much closer in frequency than C3 and C5 are, you should perceive the latter pair of tones to sound much more similar.
When two or more musical notes are played together, the combination may sound harmonious (pleasant) or discordant (unpleasant). The harmoniousness of note combinations is determined both by the ratio of frequencies of the two notes, as well as cultural factors (learning). Click the links at left to explore these two factors. Clicking each link will play a scale or a note combination and show some new text in this part of the window. You can also click the piano keys to play single notes at any time.
Instructions
Click the white and black keys on the piano keyboard to play the labeled musical notes.
Click the links below the keyboard to play some note combinations important in Western music.
The first time you visit this activity, it is best to go through each demonstration in the order they are presented at left.
Octaves
The notes you’re hearing now constitute a diatonic scale, in which the octave is divided into seven musical notes. In Western music, the notes are labeled A-B-C-D-E-F-G, and you may have learned the frequency steps associated with each note using the syllables “Do Re Mi Fa Sol La Ti Do.” (“Wait a minute,” you may be saying, “that’s eight notes, isn’t it?” True, but notice that the last note has the same syllable as the first. The second “Do” is the start of the next octave.)
Piano keyboards are organized so that in the key of C major, the seven notes of the diatonic scale are played on the white keys. Try it on the keyboard at left: click the C4 key, then the D just to its right, then E, F, G, A, B, and C5.
The black notes on a piano keyboard are “sharps” (#) and “flats” (♭), relative to the white notes. Thus, the black note to the right of C4 can be called either C# or D♭. There are five black notes mixed in with the seven white notes in a C-major scale. If you click all 12 of these notes in succession (C4, C#, D, D#, E, F, F#, G, G#, A, A#, B), you’ve played a chromatic scale.
When you move from C to C# in a chromatic scale, you are moving up one semitone. In Western music, octaves are divided logarithmically. This means that every time you go up one semitone, the ratio of the first note to the second is the same (1:1.05946). In terms of raw frequencies, it means that the first semitone of a scale (C4 to C#4) is a smaller jump (16 Hz, from 262 to 278 Hz) than the last semitone (B5 to C5, which is a 29-Hz jump from 494 to 523 Hz).
If you’re not a music major, the last paragraph will probably be quite confusing, but to your ears everything should sound simple. When you click on the “Good octave” link at left, you hear the scale divided the way you’re used to hearing it divided, and the steps sound “right.”
If you click on the “Bad octave” link, you’ll hear a diatonic scale in which the semitones are divided linearly, instead of logarithmically. Here, the raw frequency difference for each semitone is the same: going from C4 to C#4 in this scale would involve the same raw frequency jump (about 22 Hz) as going from B5 to C5.
As the link text indicates, the linear scale will probably sound “wrong” to your ears. Physically, there’s nothing right or wrong about either of these scales. But our auditory system adjusts to what it’s accustomed to hearing. If you were brought up in a Western culture, you’ve been hearing logarithmic scales all your life, so logarithmically-spaced semitones will sound pleasant and linearly-spaced semitones will sound unpleasant.
Major Fifth
Pairs of notes played together are called dyads. It appears to be generally true across cultures that note combinations having simple ratios tend to sound pleasant. Thus the major fifth, major fourth, and major third dyads, all of which have relatively simple ratios, all sound quite pleasant. This is especially true for listeners accustomed to Western music, which uses these dyads very frequently.
The major fifth dyad, which in the key of C includes the notes C and G, features a frequency ratio of 3:2 (that is, the frequency of the higher note is equal to 3/2 times the frequency of the lower note).
Major Fourth
Pairs of notes played together are called dyads. It appears to be generally true across cultures that note combinations having simple ratios tend to sound pleasant. Thus the major fifth, major fourth, and major third dyads, all of which have relatively simple ratios, all sound quite pleasant. This is especially true for listeners accustomed to Western music, which uses these dyads very frequently.
The major fourth dyad, which in the key of C includes the notes C and F, features a frequency ratio of 4:3 (that is, the frequency of the higher note is equal to 4/3 times the frequency of the lower note).
Major Third
Pairs of notes played together are called dyads. It appears to be generally true across cultures that note combinations having simple ratios tend to sound pleasant. Thus the major fifth, major fourth, and major third dyads, all of which have relatively simple ratios, all sound quite pleasant. This is especially true for listeners accustomed to Western music, which uses these dyads very frequently.
The major third dyad, which in the key of C includes the notes C and E, features a frequency ratio of 5:4 (that is, the frequency of the higher note is equal to 5/4 times the frequency of the lower note).
Minor Third
A dyad with a complex ratio tends to sound unpleasant, unless the music of the culture you’re living in happens to use the dyad very frequently.
The minor third dyad, which in the key of C includes the notes C and D#, features a frequency ratio of 6:5 (that is, the frequency of the higher note is equal to 6/5 times the frequency of the lower note).
The ratio of frequencies in a minor third dyad (6:5) is not really that much different than the ratio in a major third (5:4), so it’s interesting that the minor third sounds so much more discordant to our ears than the major third.
Augmented Fourth
A dyad with a complex ratio tends to sound unpleasant, unless the music of the culture you’re living in happens to use the dyad very frequently.
The augmented fourth dyad, which in the key of C includes the notes C and F#, features a frequency ratio of 45:32 (that is, the frequency of the higher note is equal to 45/32 times the frequency of the lower note).
This dyad may sound even worse to your ears than the minor third. As noted in the textbook, during the Middle Ages it was known as the “devil in music”. However, skilled composers can use discordant dyads and chords to make melodies more complex and interesting and therefore, on the whole, more pleasant-sounding. In the early twenty-first century, this complex dyad may be best known from Danny Elfman’s opening theme for The Simpsons—the first and third notes from the beginning of the theme form an augmented fourth.
C Major Chord
Trios of notes form a chord. As with dyads, chords tend to sound pleasant when they have simple frequency ratios.
The C major chord you hear here includes the notes C-E-G, constituting a frequency ratio of 6:5:4. This is the simplest possible ratio of three notes in a single Western diatonic scale, so it is the most harmonious chord to Western ears.
C Minor Chord
Trios of notes form a chord. As with dyads, chords tend to sound pleasant when they have simple frequency ratios.
The C minor chord you hear here includes the notes C-D#-G, constituting a frequency ratio of 15:12:10. It should sound less pleasant than the C major chord, even though just a single note changed (E to D#).
Augmented C Chord
Trios of notes form a chord. As with dyads, chords tend to sound pleasant when they have simple frequency ratios.
The augmented C chord includes the notes C-E-G#, constituting a frequency ratio of 32:25:20. It should sound even more discordant than the C minor chord.