Introduction

The pair of pictures at left form a stereo pair. When they are viewed with crossed convergence (see Activity 6.3 on Stereograms), the scene pops out in depth, with the lower teapot appearing closer to you than the upper teapot. As you’ve learned, this type of stereogram “works” because one side mimics the image that would fall on the left eye if you were actually viewing the three-dimensional scene, while the other side shows the image that would fall on the right eye.

As you’ve also learned, the resulting sense of depth (called stereopsis) you get when viewing a stereogram (or more commonly, when viewing an actual three-dimensional scene) is due to calculations of binocular disparity made by your visual system. In the images you see here, the binocular disparity is slightly larger for the upper teapot than for the lower teapot, hence the upper teapot appears farther away when viewed stereoscopically.

Until now, we have glossed over a crucial step in the process of achieving stereopsis. To calculate the binocular disparity of two matching points on the left- and right-eye images, we have to know which points actually go together. This process of achieving stereoscopic correspondence is the subject of this activity. The primary goal is to help you understand exactly why this is such an important issue for vision scientists to explore. The activity will conclude with a glimpse at how researchers believe the visual system achieves correspondence.

Instructions

Click on the “An Example” link at left for an explanation of why correspondence is a “problem” for perception researchers.

The links for “Correspondence in RDS” explain how the study of random dot stereograms has affected scientists’ hypotheses about the correspondence problem. In Part 1, click on the image to toggle between showing and hiding a close-up of a rectangular portion of the stereogram. In Part 2, click the stereogram to toggle between a black-and-white and a color-coded version of the close-up, and click on a dot in the close-up to see its corresponding dot (if there is one) in the opposite-side image.

The links for “Heuristics for Correspondence“ describe various rules of thumb that scientists believe the visual system uses in achieving stereoscopic correspondence. Click on the images in each part of this section to toggle between different versions, as described in the text.

An Example

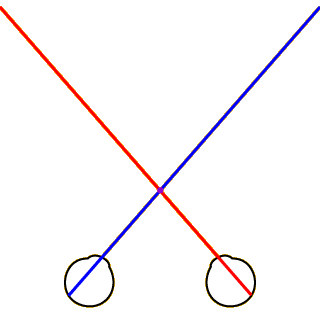
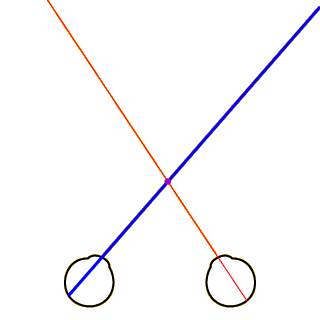
To better understand the issue of stereoscopic correspondence, consider the small sections of the images at the very tip of the teapots’ spouts, highlighted here by blue and yellow circles. The blue-outlined spout in the left eye should be paired with the blue-outlined spout in the right eye, while the two yellow-outlined spouts should be paired with each other. In other words, the blue-outlined spouts correspond to each other, as do the yellow-outlined spouts.

But how does the visual system know this? Why doesn’t it sometimes match the blue-outlined spout in the left eye with the yellow-outlined spout in the right eye? Determining which points in the left eye to match with which points in the right eye is known in the perception literature as the correspondence problem. While this is a “problem” for the researchers studying it and the teachers trying to explain it, stereoscopic correspondence obviously isn’t all that problematic for the visual system—if it were, we wouldn’t be very good at seeing things in depth!

Your first instinct may be to think that each position on the left retina should just automatically match up to the same position on the right retina. But remember that the whole point of binocular disparity is that most of the objects in your visual field do not fall on corresponding retinal points.

The next most obvious solution is to hypothesize that the visual system first analyzes the shapes of objects in each eye’s image, and then matches shapes across the two images. If we first recognized that there were two teapots in each eye’s image, we could then reason that the left-hand teapot in the left eye probably goes with the left-hand teapot in the right eye. Prior to the 1970s, this was how researchers believed the visual system proceeded. But all this changed when random dot stereograms were introduced to the field.

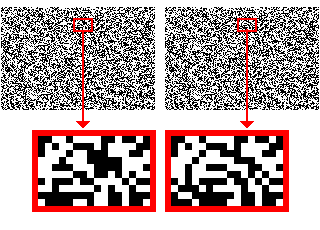
Correspondence in Random Dot Stereograms, Part 1

If you can cross-fuse the random dot stereogram (RDS) at left, you will see our two teapots again, with the upper teapot appearing farther away than the lower one. One of the intriguing things about RDSs is that no object can be seen in either the left- or the right-eye image alone—the objects can only be perceived after stereopsis has been achieved. Therefore, the discovery of RDSs effectively killed the hypothesis that calculating binocular disparity depended upon first analyzing the shapes of the objects in each eye’s image separately and then achieving stereopsis.

To appreciate just how amazing it is that the visual system can fuse RDSs, click on the RDS to see a close-up of the dots in one small portion of each image. This is the part of the RDS that contains the spout of the left-hand teapot. Which dots in the left go with which dots in the right? Most of the dots around the edges of the rectangle are fairly easy to match, but for many of the interior dots it is far from clear where the correspondence lies.

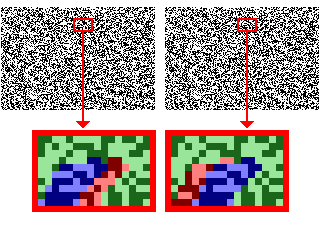
Correspondence in Random Dot Stereograms, Part 2

In this version of the close-up image, the dots are color-coded to clarify the correspondences. Click on any dot in the left-eye image to highlight its corresponding dot in the right-eye image, and click on the stereogram itself to toggle the color coding on and off.

Dark and light green dots in each image correspond to each other and form part of the background of the scene depicted in the RDS. Dark and light blue dots in each image also correspond to each other; these form the tip of the teapot’s spout. But what about the dark and light red dots? If you click on a red dot in the left image, you will find that no dot is highlighted in the right image. In fact, if you study the figure, you should see that the red dots do not have corresponding dots in the complementary image!

How can this be? One way to answer this question is to recall how RDSs are created. You start with two identical rectangles of random dots, then you cut out a pattern (here, a teapot shape) and shift these dots over in one of the two images. You then fill in the left-over space with new random dots. Non-corresponding dots are those that were either filled in or covered over in one of the images.

Another way to answer the question is to consider the three-dimensional scene that the RDS is simulating. If you can successfully cross-fuse the RDS, you will see the teapots floating above a rectangular background plane. Now consider what the two eyes would be seeing if you were looking at an actual cardboard cutout of a teapot mounted on a wall so that the teapot was a foot closer to you than the wall. Since your left eye is (by definition) located somewhat to the left of the right eye, the left eye would be able to see a small sliver of the wall behind the teapot that the right eye would not be able to see. Similarly, there would be a small sliver of wall that was visible to the right eye but invisible to the left eye. These two slivers would be the portions of the left- and right-eye images that do not have corresponding points on the other eye’s image.

Heuristics for Correspondence, Part 1

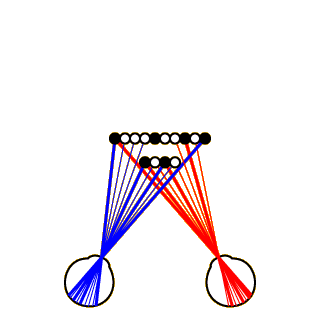
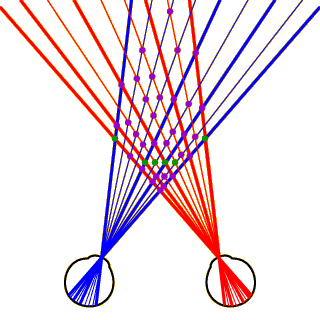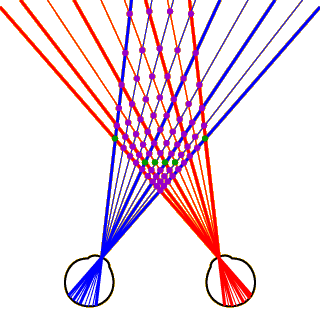
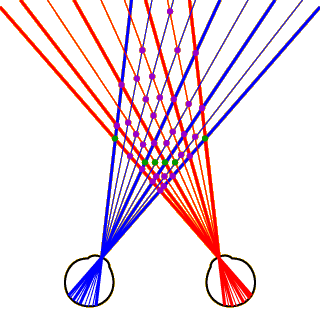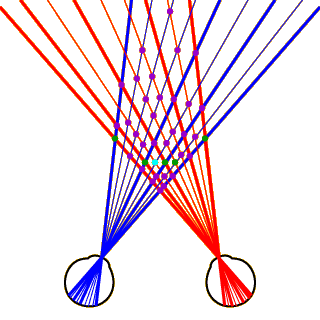
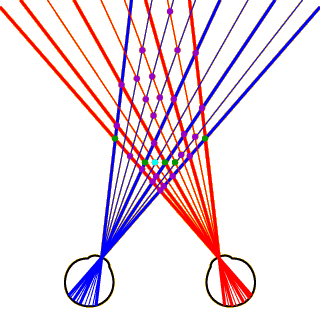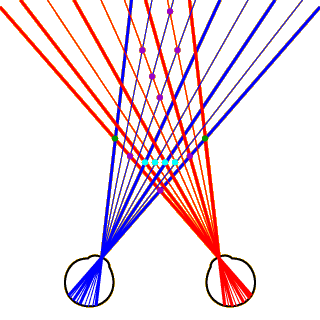
Now let’s consider how the visual system achieves proper correspondence between dots in left- and right-eye views. The image at left shows a top view of a set of disembodied eyeballs looking at a long row of black and white dots in the background with a smaller row of dots in the foreground.

Click on the image to see how these dots would project onto the left (blue lines) and right (red lines) retinas. Image projections from black dots are represented by thick lines and projections from white dots by thin lines (this will become important later on).

As you can see, all the dots in the foreground project into both eyes. This is not true of the dots in the background, however. The dots on the far left and right project into both eyes, but the two dots in the very center project to neither eye (these dots are completely occluded by the foreground dots). Most of the other dots in the background project to one eye or the other, but not to both.

Heuristics for Correspondence, Part 2

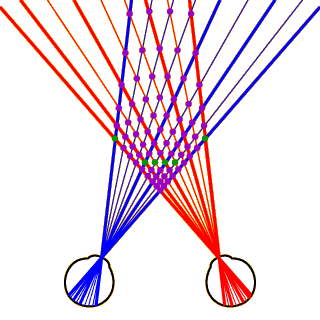
Now click anywhere in the image at left to see all the potential matches that could be computed given these left- and right-eye images. There are 81 potentially corresponding points (6 of the 81 are not shown in the image, because they would fall off the top of the screen). Only 6 of these potential matches represent points that actually correspond to each other. These 6 “true matches” are shown in green. The other 75 potential matches are “false matches,” and are shown in purple.

This figure is a bit daunting when you first see it, so click anywhere in the image to hide all but one of the potential matches. This is a false match, formed by combining the farthest-left dot in the right eye with the farthest-right dot in the left eye.

So how does the visual system filter out the correct matches from the incorrect ones? Although the details have not all been worked out, researchers believe that the visual system does so by applying certain heuristics (rules of thumb) that serve to constrain the problem in important ways.

Heuristics for Correspondence, Part 3

Consider the false match that we’ve isolated here. Note that the line passing through this match to the left eye is thick, meaning that it is a projection of a black dot, while the projection to the right eye is thin, representing a white dot. This cannot be: The illumination of any point in the world should be the same on both eyes, so a black dot in one eye cannot correspond to a white dot in the other eye.

This provides us with our first important heuristic, called compatibility. Formally, we can state this heuristic as follows: “For any given point on the right retina to correspond to any given point on the left retina, the points must have compatible illuminations.” There are other forms of compatibility (e.g., lines should have the same orientation if they match), but we’ll stick with illumination for the present demonstration.

Click on the image to see the false matches that we can eliminate via the compatibility heuristic. Many false matches remain, but we’ve already gotten rid of over half of them.

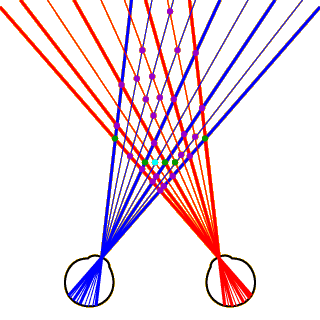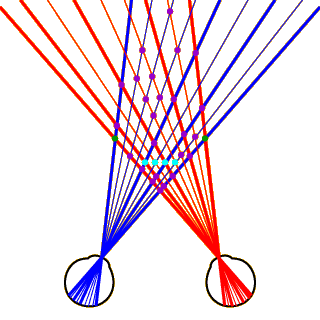
Heuristics for Correspondence, Part 4

Let’s assume that our disembodied eyeballs are focusing on the center-left dot in the foreground, the one that you see flashing. If this dot falls precisely in the center of the fovea of both retinas, we know that it is a true corresponding point.

Given this knowledge, we can apply a second heuristic, called uniqueness: “A given feature in one image can only match one feature in the other image.” The uniqueness heuristic tells us that all the other potential matches that fall on the two projection lines passing through the true match must be false. This is more complicated than it may sound; click on the image to see the matches we can eliminate in this way.

Heuristics for Correspondence, Part 5

Finally, consider the continuity heuristic: “Disparity should generally change smoothly, since continuous surfaces are more common in a scene than sharp discontinuities.” All this means is that once we’ve established one true match in an image, it’s likely that potential matches that fall just to one side or the other are probably also corresponding points.

Given this heuristic, we can make an educated guess that the points you see flashing now are also true matches. Then, reapplying the uniqueness heuristic for these newly-established true matches, we can eliminate some other points (click the image to see these points eliminated).

We are now down to 17 potential matches, of which we know 4 are true matches. By continuing to use all the heuristics we’ve discussed so far, as well as others that are too complicated to explain here, the visual system matches all the corresponding points, eliminates all the false matches, and achieves stereopsis.