Chapter 6 Overview

Space Perception and Binocular Vision

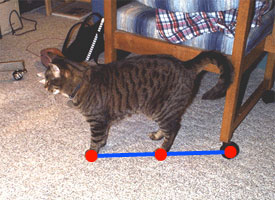
Measuring distances in the picture plane—the plane running from left to right and top to bottom in front of your face—is a fairly straightforward job for the visual system. For example, in the picture of Penny the cat in Figure 1, it is easy to see that the distance between Penny’s front and back paws is about the same as the distance between her back paw and the chair leg (click the image to show lines making this point more clear).

 

Figure 1  Distance in the picture plane is easy to determine ... (Click to toggle between two versions of this image.)

This is because the distance between Penny’s front paw and back paw on your retina is the same as the distance between her back paw and the chair leg. In the picture plane, retinal distance is proportional to distances in the “real world.” No problem.

However, when measuring distances in other planes, the visual system does have a problem. For instance, consider Penny in Figure 2. Here, the distance on the retina between Penny’s two ears is nearly identical to the distance between her left ear and the tip of her tail (click the image to make these retinal distances more explicit). But despite the similarities in distance in the retinal image, your brain knows that in all three dimensions, the ear-to-ear distance is probably much smaller than the ear-to-tail distance.

Figure 2  ... but distance in other planes is considerably more difficult. (Click to toggle between two versions of this image.)

Like so many “problems” we discuss in this textbook, the visual system is remarkably good at solving this one. We routinely construct accurate representations of three-dimensional space from two-dimensional retinal images. As we see here, and as you prove every time you accurately perceive depth relations in any TV show, movie, photo, or painting, it is possible to work out this representation of space based solely on monocular depth cues (Activity 6.1)—cues that are available even if you view the world, or a photo, with only one eye. Essay 6.1 – Making the Implicit Explicit discusses how artists over the ages have “discovered” these depth cues one by one.

But while monocular depth cues are good enough in most cases, the real world pops out at you in depth like no two-dimensional image can, as long as you have both eyes open (try walking around with one eye closed for a while and you’ll begin to see how much flatter the world looks without two eyes). The reason for this enhanced experience of depth is that your two eyes give you two slightly different views of the world, as demonstrated in the activity on binocular disparity (Activity 6.2), leading to another depth cue called stereopsis. In modern times, we’ve learned to simulate binocular disparity using devices called stereoscopes and images called stereograms; these can be explored in Activity 6.3 and Essay 6.2 – Stereo Images on the Web.

The final activity for this chapter, Activity 6.4 – Stereoscopic Correspondence, covers a complexity in stereopsis known as the correspondence problem, and the final essay, on Essay 6.3 – The Moon Illusion discusses one of the many illusions that come about when we make mistakes in perceiving depth relations.

Once you’ve read the chapter in the textbook and done the activities here, use the study aids (Study Questions, Flashcards, and Chapter Summary) to review.