Introduction: Harmonic Sounds

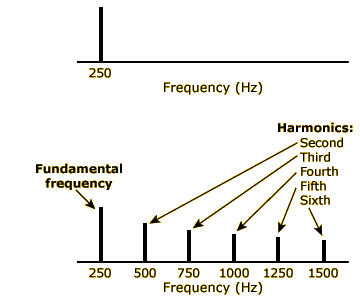
Most of the sounds used in our web activities so far have been simple tones—sounds created by a computer program in which the sound pressure level oscillates back and forth at a single frequency according to a sine wave function. Simple tones are nice to use in demonstrations and laboratory experiments because they’re easy to generate, manipulate, and describe. You can hear another simple tone, which has an amplitude of 250 Hz, by clicking on the top speaker at left.

But in the real world, most sounds are complex, meaning that they are made up of multiple frequencies. In Chapter 1, in the activity on Fourier Analysis, we saw how a complex tone can be broken down into a series of simple tones, with each simple tone component having its own frequency.

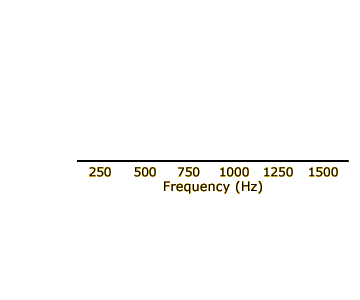
Click the bottom speaker at left to hear another complex sound. As shown by the sound spectrum to the right of the speaker, this sound is made up of components that have frequencies of 250, 500, 750, 1000, 1250, and 1500 Hz. Notice that these frequencies are all integer multiples of a single number: 250 = 1 × 250, 500 = 2 × 250, 750 = 3 × 250, and so on. In mathematical terms, we say that 250 is the least common denominator (LCD) of the component frequencies.

Complex sounds in which all components share an integer LCD are said to have a harmonic structure. The 250-Hz component is called the fundamental frequency of the sound, the next-highest component (500 Hz) is called the second harmonic, the next-highest component (750 Hz) is called the third harmonic, and so on.

We saw back in Chapter 9 that a sound wave’s frequency is the primary determinant of a psychological property called pitch, which we associate with musical notes. When a complex sound has a harmonic structure, our auditory system always bases pitch perception on the fundamental frequency. The two sounds in this part of the activity prove this point. You should perceive them as having the same pitch (which will be close to a middle B note), since one is a 250-Hz simple tone and the other is a complex, harmonic tone with a 250-Hz fundamental frequency. That’s not to say that you will hear the tones as being identical. The amplitude and timbre of the tones clearly differ. But pitch-wise, you should hear the similarity between them.

Missing Fundamentals

In the introduction to this activity, we learned that the pitch of a complex harmonic tone is based on the fundamental frequency of the tone, the least common denominator. Click the speaker at left to hear the same complex tone from the Introduction, which takes on the pitch of its fundamental frequency, 250 Hz.

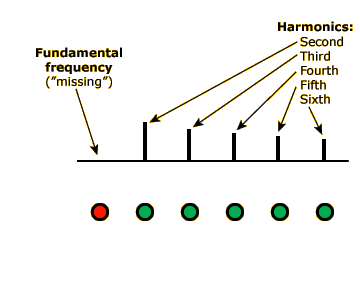
Now, what do you think would happen if we took the 250-Hz component out of this complex tone? A reasonable guess would be that the pitch of the tone would rise, since 500 Hz would now be the lowest-frequency component of the tone.

But remember that the fundamental frequency is defined as the LCD (least common denominator) of the component frequencies in a complex tone. As it turns out, pitch is based on this LCD even if the LCD frequency itself—the fundamental frequency—is missing from the tone! Therefore, our new tone should have the same pitch as the old one.

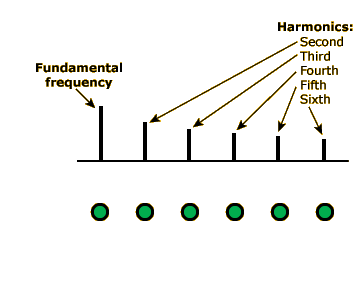
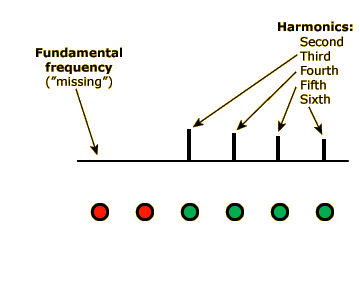
Click the small green circle under the 250-Hz component of the spectrum to toggle this component off, and you will hear this principle in action. Again, the two tones (the full complex sound with the 250-Hz component and the complex sound without the 250-Hz component) will not sound identical, but they will have the same pitch.

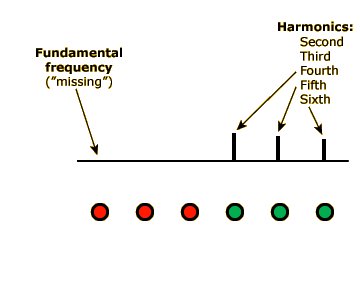
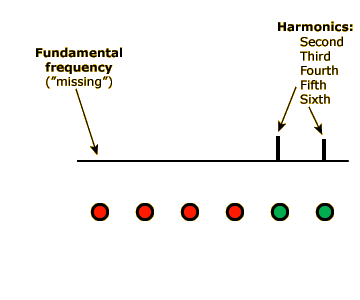
Now click the other small green circles to toggle the 500-Hz, 750-Hz, and 1000-Hz components off. In each case, the tone should remain the same pitch. Even when the only two components are 1250 Hz and 1500 Hz, the complex tone will still take on the pitch of a pure 250-Hz tone, because 250 is the LCD of 1250 and 1500 (1250 = 250 x 5; 1500 = 250 x 6).

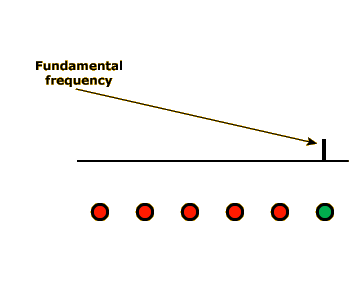
If you remove the 1250-Hz component, the pitch will finally change. At this point, 1500 Hz will be the only, and therefore the fundamental, frequency of the tone, and the pitch will shift from middle B to a high F#. You may want to toggle the 1250-Hz component on and off a few times to convince yourself that these two pitches really are different.

More Missing Fundamentals

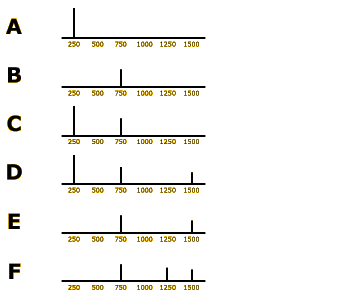
In this part of the activity, we have six different tones, labeled A through F. See if you can predict from their spectra what the fundamental frequency of each tone will be. For each tone, first make a prediction, then click the speaker to hear the tone and show an analysis of why it has the pitch that it does.

The first time you do this part of the activity, you should probably go through the six tones in order from A to F.

Tone A

Tone A should be easy, since we already encountered this tone in the first part of the exercise. Since 250 Hz is the only component, it is the fundamental frequency, and the tone’s pitch will be heard as 250 Hz.

Tone B

As with tone A, tone B includes only one component, so this component will determine its fundamental frequency and pitch: 750 Hz.

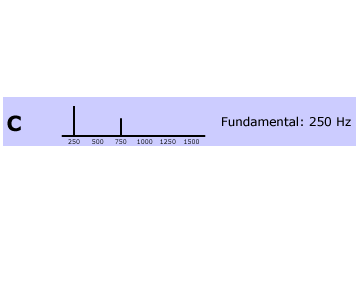
Tone C

Tone C has two components, 250 Hz and 750 Hz. The least common denominator of these two frequencies is 250, so the complex tone’s pitch will be 250 Hz. Therefore, Tone C should sound more similar to Tone A than Tone B.

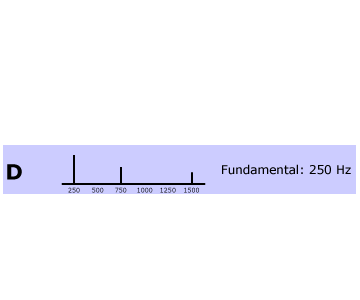
Tone D

In tone D, we’ve added a 1500-Hz component to the 250-Hz and 750-Hz components in tone C. The least common denominator is still 250, so the complex tone’s pitch will still be 250 Hz, making it sound more similar to Tone A than Tone B.

Tone E

In tone E, we’ve taken tone D and removed the 250-Hz component. For the two remaining components, 750 Hz and 1500 Hz, 750 is the LCD, so it will be the fundamental frequency, and the pitch will be 750 Hz. This tone sounds more similar to Tone B than Tone A.

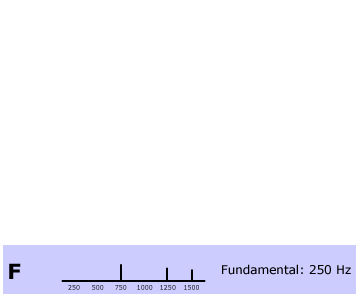
Tone F

In our last sound, tone F, we’ve added a 1250-Hz component to tone E. The least common denominator of 750, 1250, and 1500 is back to 250 (it’s not 750 any more, because 1250 / 750 is 1.67, not an integer), so this will be the fundamental frequency, and the pitch shifts back to 250 Hz, and sounds more like Tone A than Tone B.

The contrast between tones E and F is particularly interesting. In moving from E to F, we added a high-frequency tone (1250 Hz), yet the perceived pitch of the complex tone as a whole shifted down, because the fundamental frequency went from 750 down to 250 Hz.