Essay 2.2 How Many Quanta Does It Take?
On a dark night you notice your favorite distant star out of the corner of your eye. It seems very dim, so you turn your eye to look at it directly (with your fovea), and it disappears! Why did it disappear? Because rods are more sensitive to dim light than cones, and there are no rods in your fovea. Since your rods are most numerous at 15° to 20° of visual angle away from the fovea, it is not surprising that you see the dim star most vividly out of the corner of your eye.
Only about one-half of the photons (also known as “quanta”) from a star that arrive at the cornea make it to the retina, and those that do are spread by the eye’s optics (which are only slightly worse at 15° to 20° than they are in the fovea).
Signals and Noise
Of course, the light from our favorite star is spread over many rods by the eye’s optics, and for us to reliably detect a dim star, a number of rods need to be active at the same time. We explained earlier that if you record electrical potentials from a ganglion cell, occasionally the ganglion cell fires “spontaneously” when there is no light present. Since ganglion cells signal to the brain what they see by changing their firing rate, the brain must distinguish between spikes fired in response to a stimulus (the “signal”) versus spontaneous firing (the “noise”).
Rods also have spontaneous electrical events that are not distinguishable from their normal responses to light. If you are in the dark and close your eyes, you can sometimes see these spontaneous events as little shimmering specks of light. Spontaneous electrical changes in visual neurons—noise—acts like light and is sometimes referred to as “dark light” or “equivalent light.”
Imagine that your job is to detect a dim star out of the corner of your eye (where your rods are most dense). Although we know that a rod can signal the absorption of a single quantum of light, spontaneous noise would send an indistinguishable signal. So to be able to reliably detect the star you have to distinguish between signals generated by photons absorbed from the star and noise generated by spontaneous electrical events. This signal-to-noise problem requires that at least a few quanta are absorbed by a few rods in the region of the retinal image of the star within a “shutter time” of approximately one-tenth of a second.
How Many Quanta Does It Take?
Answering this question requires a more controlled experiment than simply trying to spot a star out of the corner of your eye. In order to make a precise estimate of the smallest number of quanta needed to reliably detect a light, we need to be able to precisely control both the stimulus and the state of the observer. Fortunately, Hecht, Schlaer, and Pirenne (1942) conducted such an experiment about 65 years ago, and their approach, results, and analysis still tell us much about the way our visual system operates.
Hecht et al. were interested in determining the smallest number of quanta needed to reliably detect a visual target. Since rods are sensitive to dim lights, they presented the target to the region of the retina with the highest density of rods (about 20° in the temporal retina) under the reasonable assumption that sensitivity should be highest where the density of rods is highest.
It Takes Fewer Quanta After About 30 Minutes in the Dark
Before beginning the test, Hecht et al. had their observers sit in the dark for about 40 minutes. While sitting in the dark for 40 minutes is not as bad as wandering in the desert for 40 days and 40 nights, it is still not much fun. So why did they do it? You have probably noticed that when you go from a brightly lit environment into a dark one (such as a movie theater) it takes you a while to be able to see. This is the phenomenon known as dark adaptation. Image 1 shows how sensitivity increases up to about 30 minutes in the dark. At this point dark adaptation is complete and the observer’s sensitivity is highest.
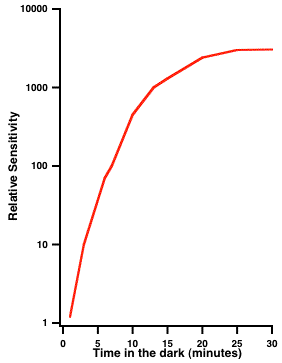
Image 1 Relative sensitivity increases with time in the dark. The curve demonstrates that sensitivity at 20 degrees in the periphery (where rod density is highest) increases with time in the dark.
Hecht et al. chose a test target that was small (subtending 10 minutes, or one-sixth of a degree of visual angle), brief (1 ms), and monochromatic (wavelength of 510 nm). Below, we will explain why; however, the main point is that Hecht et al. chose conditions under which neither the size nor the duration of the target mattered—only the number of quanta.
There Is a Critical Size Below Which Only the Number of Quanta Matter
Image 2 plots the number of quanta required to detect briefly flashed spots of light of different sizes (diameters). Note that at this test location, for targets less than about 10 minutes in diameter, the number of quanta is constant but that for larger targets the number of quanta increases. Thus, a spot of about 1 minute in diameter can be detected with the same number of quanta as a spot of 10 minutes in diameter. For spots smaller than the “critical diameter” (shown by the “corner” of the function at 10 minutes), we can trade off the intensity of the spot with its size to maintain a constant number of quanta. This ability to trade off area and intensity is sometimes called “Ricco’s law” and the critical diameter is known as “Ricco’s diameter.” Image 3 shows that Ricco’s diameter measured under both scotopic (rod) conditions (Scholtes and Bouman, 1977—purple dots) and under photopic (cone) conditions (Webber, 1988—green dots) depends on eccentricity.
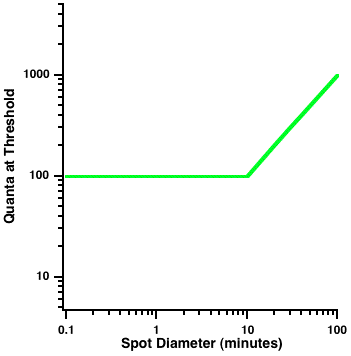
Image 2 Ricco’s law. This figure plots the number of quanta required to detect a briefly flashed spot of different sizes (diameters). For targets less than about 10 minutes of visual angle, the number of quanta is constant; however for larger targets the number of quanta increases. The “corner” at 10 minutes of visual angle defines Ricco’s diameter. For spots smaller or equal to Ricco’s diameter, only the number of quanta matter.
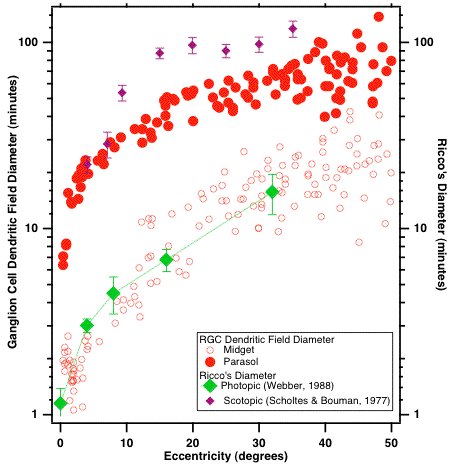
Image 3 Ricco’s diameter measured under scotopic (rod) conditions (from Scholtes and Bouman, 1977—purple diamonds) and under photopic (cone) conditions (from Ann Webber’s masters thesis, 1988—green diamonds) increases with eccentricity. For comparison, the open red dots show the size of the dendritic fields of P ganglion cells and the solid red dots show the size of the dendritic trees of M ganglion cells (from Dacey and Peterson, 1992).
Interestingly, the sizes of Ricco’s diameter determined psychophysically under photopic conditions are remarkably similar to the dendritic fields of P ganglion cells measured in humans by Dacey and Peterson (1992). Ricco’s diameter under scotopic conditions is similar to or slightly larger than the size of M ganglion cell dendritic fields. Thus, Ricco’s diameter likely reflects summation of quanta by the large number of rods that are connected to each retinal ganglion cell. Since the number of photoreceptors connected to each retinal ganglion cell increases with retinal eccentricity, so does the size of Ricco’s diameter. At an eccentricity of 20° (where Hecht et al. placed their stimulus), there are estimated to be about 250–500 rods in the area covered by Hecht et al.’s 10 minute of visual arc spot of light. As long as all the quanta are restricted to falling within Ricco’s diameter, it does not matter how they are spatially distributed. Hecht et al. could just as easily use a stimulus area of 1 minute of arc; however, they chose 10 minutes (still within Ricco’s diameter) for technical reasons.
There Is a Critical Duration below which Only the Number of Quanta Matter
Image 4 shows why Hecht et al. chose their brief stimulus duration. This figure plots the total number of quanta required to detect a small target flashed for different stimulus durations. For durations less than about 0.1 sec, the total number of quanta is constant; however, for longer durations the number of quanta increases. For durations less than the “critical duration” (shown by the “corner” at 0.1 sec), we can trade off the intensity of the spot with its duration in order to maintain a constant number of quanta. This ability to trade off duration and intensity is sometimes called “Bloch’s law.” Just as Ricco’s diameter tells us that there is spatial summation of quanta within a fixed area, Bloch’s law tells us that there is also temporal summation of quanta within a fixed time. In a sense, you can consider the critical duration for human vision to be analogous to the shutter time on your camera.
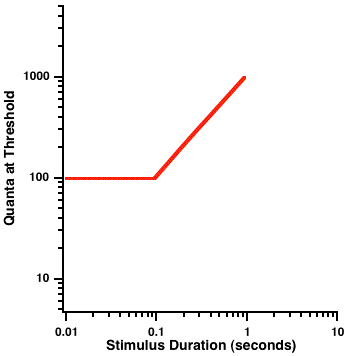
Image 4 Bloch’s law. This figure plots the total number of quanta required to detect a small target flashed for different stimulus durations. For durations less than approximately 0.1 s, the total number of quanta is constant; however, for longer durations the number of quanta increases. The “corner” of the function at 0.1 s defines the “critical duration.” For durations less than the “critical duration,” we can trade off the intensity of the spot with its duration in order to maintain a constant number of quanta. This ability to trade off duration and intensity is called Bloch’s law.
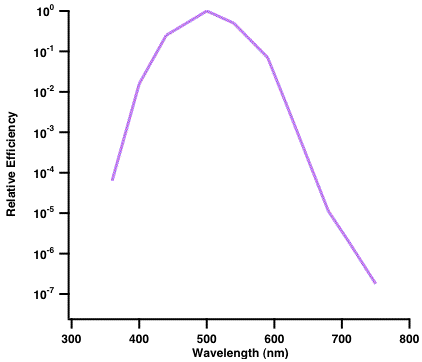
Image 5 The action spectrum of rhodopsin. Rhodopsin is most efficient at capturing quanta with wavelengths of about 510 nm.
Rods Are Optimally Sensitive to Wavelengths Approximately 510 nm
Under low light levels, rods are more sensitive than cones. Rods have a single photopigment called rhodopsin, which is not an equal opportunity photopigment: It captures quanta with a wavelength of about 510 nm more efficiently than quanta of either longer or shorter wavelengths. The curve in Image 5 shows the action spectrum of rhodopsin (i.e., how efficiently rhodopsin captures quanta of different wavelengths). Under scotopic conditions, human sensitivity to briefly flashed lights of different wavelengths closely follows the action spectrum of rhodopsin. Thus, humans require fewer quanta to detect a 510 nm light than either a 400 or a 600 nm light. As discussed in the chapter on color perception (Chapter 5), under scotopic (rod) conditions, near-threshold light appears colorless or gray. Since Hecht et al. were interested in the smallest number of quanta that could be detected, they chose quanta with a wavelength of 510 nm, on the assumption that these quanta would be captured, and therefore detected, most efficiently.
So, How Many Quanta Does It Take to See?
Hecht et al. found that their observers could detect a small, brief, flash of wavelength 510 nm 60 percent of the time when it contained around 90 quanta. As we noted earlier, some of those 90 quanta will be reflected by the cornea (approximately three), and only about one-half of the remaining 87 quanta will actually reach the rods. Not all of the approximately 44 quanta reaching the rods will be absorbed (we rounded up because you can’t have a fraction of a quantum). Some will fall between the cracks (i.e., some quanta will land in the spaces between the rods), and not all of the quanta entering rods will be absorbed. Hecht et al. estimated that no more than 20 percent of the quanta landing on the retina will be absorbed. Under these assumptions, their observer could detect a flash when just nine quanta were absorbed! Recall that the flash covered a diameter of ten minutes of visual angle on the retina (and thus several hundred rods), so, Hecht et al. concluded that their observer detected the stimulus when about nine rods in the area of the flash each absorbed a single quantum! Although some of their assumptions have been challenged, their main conclusion, that a single quantum can activate a rod, remains one of the fundamental discoveries about the limits of human vision.
Interestingly, it appears that cones are also able to capture single photons; however, their electrical responses are weak and noisy.
References
Dacey, D. M., and Peterson, M. R. (1992). Dendritic field size and morphology of midget and parasol ganglion cells of the human retina. Proc Natl Acad Sci 89: 9666–9670.
Hecht, S. Schlaer, S., and Pirenne, M. H. (1942). Energy, quanta and vision. J. Opt. Soc. Am. A. 38: 196–208.
Scholtes, A. M., and Bouman, M. A. (1977). Psychophysical experiments on spatial summation at threshold level of the human peripheral retina. Vision Res 17: 867–873.